Siempre hay una recta para cualquier reloj
Demostramos que pintemos como pintemos los doce números (siempre seis rojos y seis azules) habrá una recta que divida por la mitad la esfera dejando tres de cada color en cada lado
Elisa Lorenzo, estudiante de doctorado de la Politécnica de Cataluña, plantea y resuelve el cuarto desafío matemático de EL PAÍS con el que celebramos el centenario de la Real Sociedad Matemática Española(ver vídeo del planteamiento a la izquierda de la página y vídeo de la solución a la derecha). Para evitar dudas y en atención también a nuestros lectores sordos incluimos la demostración por escrito y otras posibles soluciones que han enviado nuestros lectores. El ganador esta semana de una biblioteca matemática como la que cada domingo difunde EL PAÍS es Olivier Georg, que reside en Andoáin (Guipúzcoa). En total han llegado 1.273 soluciones, aproximadamente la mitad de ellas correctas. Hoy plantearemos un nuevo problema.
Recordemos que el problema pedía demostrar que si pintamos los doce números de un reloj con dos colores, seis de rojo y seis de azul, siempre habrá una recta que divida la esfera en dos mitades dejando tres de cada color en cada uno de los lados. Esta es la solución que propone Elisa Lorenzo. Muchos lectores han llegado a la misma demostración o a otras análogas.
Partamos de una recta cualquiera que divida al reloj por la mitad dejando 6 números a cada lado. Y seleccionemos una de las dos mitades. Fijémonos en el número de números pintados de rojo en dicha mitad, si este número fuese 3, esta recta cumpliría ya las condiciones del problema. Supongamos pues que no es 3, y que por ejemplo es 4. Entonces en la otra mitad habrá 6 - 4 = 2 números pintados de rojo.
Vayamos girando la recta en el sentido de las agujas del reloj poco a poco, de modo que vamos dejando un número fuera de la mitad inicial y vamos cogiendo un número nuevo. En esta nueva mitad el número de números rojos será, el mismo si hemos quitado y añadido números del mismo color, o habrá variado en más o menos uno si hemos añadido y quitado números de distinto color.
Cuando hayamos girado la recta 180º estaremos considerando la mitad opuesta a la primera que habíamos considerado, que tenía 2 números pintados de rojo. Luego nos hemos movido de una mitad que tenía 4 números pintados de rojo a una que tiene 2 números pintados de rojo moviéndonos de uno en uno, así necesariamente hemos pasado por una mitad que tenía 3 números pintados de rojo. La recta que determinaba esta mitad cumple las condiciones pedidas por el problema.
Si la mitad inicial hubiese tenido 0, 1, 2, 5 ó 6 números pintados de rojo el razonamiento es completamente análogo.
Algunos lectores han enviado soluciones basadas en la casuística, como esta que nos ha mandado Jesús García Gual.
En vez de rectas hablaremos de diámetros que dividen el círculo en dos semicírculos, cada uno con seis números.
Vayamos consiguiendo acercamientos al resultado. Podemos suponer que hay dos números seguidos (el 12 y el 1 se consideran seguidos) con igual color, ya que si no, los colores serían alternados y cualquier diámetro que no pisa números verifica lo que queremos. Así que sin perder generalidad supongamos que el 3 y el 4 son rojos. Trazamos un diámetro que pase entre 2 y 3.
Si desde 3 hasta 8 sólo el 3 y 4 son rojos, significa por un lado que del 5 al 8 son azules, y que del 9 al 2 hay cuatro rojos y dos azules. Si el 2 es rojo, resolvemos el problema girando el diámetro cogido 30º alrededor del centro de la circunferencia en sentido antihorario (trazamos un diámetro entre 1 y 2). Si el 2 es azul y el 1 rojo, habrá que girar un ángulo de 60º (diámetro entre 12 y 1). Y si el 2 y el 1 son azules el giro de 90º resolverá el problema (diámetro entre 11 y 12).
Si desde 3 hasta 8 sólo hay tres rojos (el 3 y el 4 y otro más) nuestro diámetro nos vale.
Si desde 3 hasta 8 sólo hay cuatro rojos, de 9 a 2 hay sólo dos rojos. Si 9 es azul, bastará con girar nuestro diámetro 30º en sentido horario (diámetro entre 3 y 4). Si 9 es rojo y 10 azul, giraremos 60º (diámetro entre 4 y 5). Si 9 es rojo y 10 rojo, entonces entre 9 y 2 hay dos rojos seguidos (9 y 10) y sólo dos rojos, luego ya estamos en un caso estudiado y resuelto.
Si desde 3 hasta 8 hay sólo cinco rojos, desde 9 hasta 2 hay un solo rojo. Si 2 es rojo, giramos el diámetro de partida 60º en sentido horario (diámetro entre 4 y 5). Si 2 es azul y 1 es rojo, giramos también 60º (entre 4 y 5). Si 2 y 1 son azules, entonces entre 1 y 6 hay dos rojos seguidos (3 y 4) y tres o cuatro rojos (casos ya estudiados).
Si desde 3 hasta 8 los seis son rojos, bastará con trazar un diámetro perpendicular al de partida.
Por último, destacamos por su originalidad y sencillez la solución presentada por María Teresa Trobajo de las Matas.
Dividimos el reloj en cuatro partes iguales, con dos rectas que pasan por el centro. Una de estas dos rectas va a ser solución del problema en la mayoría de los casos. Denotamos a estas partes (1), (2), (3) y (4). Cada una de estas partes contiene tres números:
(1)|(2)
_____
(3)|(4)
Contamos cuántos números de un determinado color (por ejemplo ROJO) hay en cada parte. Las diferentes posibilidades son soluciones de:
x1+x2+x3+x4=6 con 0 <=xi<=3
Construimos la recta para las distintas soluciones de esta ecuación:
(a) Solución (3,3,0,0) y todas sus permutaciones: TRIVIAL. Una de las dos rectas iniciales es válida, pues separa 3+0 Rojos de otros 3+0.
(b) Solución (3,2,1,0) y todas sus permutaciones:
*Si 3 y 0 son contiguos, como en el caso anterior, una de las dos rectas es válida, separa 3+0 Rojos de otros 2+1.
*Si 3 y 0 no son contiguos, están en cuadrantes enfrentados, por ejemplo
3|1
_____
2|0
se resuelve tomando la recta que divide el cuadrante que tiene 3 rojos, pasando uno al contiguo que tiene 2 y dos al contiguo que tiene uno.
(c) Solución (3,1,1,1) y sus permutaciones: contando azules serían (0,2,2,2). Tomando la recta que divide a los dos azules del cuadrante enfrentado con el que no tiene azules, se acaba.
(d) Solución (2,2,2,0) y sus permutaciones: Como el anterior.
(e) Solución (2,2,1,1) y sus permutaciones: Una de las rectas que dividen los cuadrantes es válida, pues divide 2+1 Rojos y 2+1 Rojos.
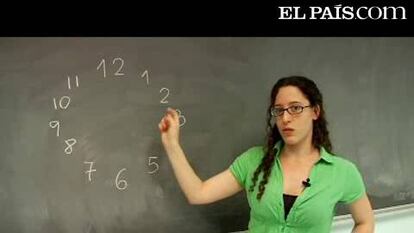
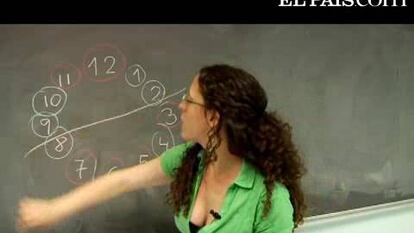
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.




























































