Dos triángulos idénticos
El ganador del 39º desafío matemático es José María Vaquero Guerri, de Madrid
Ya hay solución para el trigésimo noveno desafío matemático con el que EL PAÍS celebra el centenario de la Real Sociedad Matemática Española.
Miguel Ángel Morales Medina, licenciado en Matemáticas por la Universidad de Granada y editor del Boletín de la RSME, propuso este penúltimo desafío (ver vídeo de la izquierda) y ahora lo resuelve (vídeo de la derecha). Recordemos en qué consistía.
Partiendo de un triángulo cualquiera de vértices ABC, tomamos dos de sus lados, AB y AC por ejemplo, y dibujamos cuadrados apoyados en ellos. Llamamos I y J a los centros de los dos cuadrados y H al punto medio del lado del triángulo donde no hemos apoyado ningún cuadrado (el BC en este caso). Se pedía demostrar que los segmentos HI y HJ tienen la misma longitud y que además forman un ángulo de 90º.
Esta semana se han recibido 285 respuestas dentro del plazo, la gran mayoría de ellas, el 95%, correctas. Las que se han considerado como incorrectas lo son principalmente porque alguna de las demostraciones pedidas no se ha hecho con suficiente claridad o simplemente no se ha hecho. Respecto al tipo de soluciones recibidas, lo más destacable es la tremenda variedad de soluciones que se han enviado para este desafío. Podríamos citar cerca de una decena de formas distintas de resolverlo, aunque algunas de ellas son equivalentes. El ganador de una de biblioteca matemática como la que entrega cada semana EL PAÍS ha sido en esta ocasión José María Vaquero Guerri, de Madrid.
La solución que se presenta en el vídeo es posiblemente la más simple de todas las que conocemos para este problema, en el sentido de que es la que necesita de unos conocimientos más básicos: semejanza de triángulos y un poco de vista. Veamos cómo hacerlo.
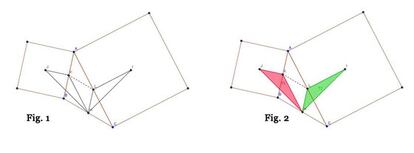
Llamemos K al punto medio del lado AB y L al punto medio del lado AC, y dibujemos los triángulos HKJ y HLI. Representamos también el segmento KL en línea discontinua (ver la figura 1 en la parte superior o la ampliación aquí).
Como el segmento LH une los puntos medios de los lados AC y BC, entonces es paralelo al otro lado, el AB. Lo mismo ocurre con el segmento KL, que como une los puntos medios de los lados AB y AC será paralelo al otro lado, el BC. Esto nos dice que BHLK es un paralelogramo, por lo que, en particular, los segmentos KB y LH son iguales. Pero KB y JK también son iguales, por lo que obtenemos que JK=LH. El mismo razonamiento nos sirve para llegar a que ALHK es un paralelogramo, por lo que, en particular, los segmentos AL y KH son iguales. Pero AL y LI también lo son, por lo que ahora se obtiene que KH=LI.
Por otro lado, los triángulos KBH y LHC tienen sus lados iguales y paralelos, por lo que el ángulo BKH y el ángulo HLC son iguales.
Recapitulemos. Tenemos que los triángulo JKH y el HLI (pintados de rojo y verde respectivamente en la figura dos, que aparece aquí ampliada) tienen dos lados iguales (KJ=LH y KH=LI) y además también tienen igual el ángulo formado por esos lados (el ángulo JKH es 90º+BKH, y el HLI es 90º+HLC, que hemos visto antes que es igual a BKH). Con esto podemos concluir que ambos triángulos son iguales, y el hecho de que sean iguales nos asegura que los segmentos HI y HJ tienen la misma longitud.
Falta demostrar que estos dos segmentos forman un ángulo de 90º. Pero esto es sencillo: JK forma un ángulo de 90º con AK, que es paralelo a LH. Por tanto JK y LH forman un ángulo de 90º. Del mismo modo, LI forma un ángulo de 90º con AL, que es paralelo a KH. Por tanto LI y KH forman un ángulo de 90º. Como los triángulos son iguales, todo esto nos asegura que los segmentos HI y HJ forman un ángulo de 90º.
Otras soluciones
Aunque ha habido una buena cantidad de respuestas con esta solución, no ha sido la más frecuente. La respuesta correcta más repetida ha sido una demostración vectorial, siendo Juan José Gibaja Martins quien la envió en primer lugar. Podríamos resumirla así: colocamos el origen de coordenadas en el punto medio del lado donde no se apoyaba ningún cuadrado, el punto H en la figura, y calculamos las coordenadas de los vectores HI y HJ que unen el origen con los dos centros de los triángulos. Después se calcula el módulo de esos vectores obteniendo el mismo resultado, hecho que demuestra la primera cuestión del desafío. Para la segunda se utiliza que si el producto escalar de dos vectores en el plano es nulo (como es el caso) entonces los vectores son ortogonales, es decir, forman un ángulo de 90º. En la línea del cálculo vectorial también ha habido respuestas que se salieron del plano para adentrarse en el espacio tridimensional, como la de José Luis Tetuán Goñi, que usó un vector perpendicular al plano de la figura y que el producto vectorial de dos vectores nos da como resultado un vector perpendicular a los dos.
Otra de las respuestas relativamente frecuente ha estado relacionada con los números complejos, concretamente con la siguiente propiedad: multiplicar un número complejo por i lo que hace es girarlo 90º en sentido antihorario. Fijando entonces el centro de coordenadas en H, como antes, y demostrando que el número complejo que representa a J es igual al número complejo que representa a I multiplicado por la unidad imaginaria i tenemos demostradas las dos partes del desafío. José Luis Arregui Casaus fue el primero que envió este tipo de solución.
Ha habido más soluciones realmente interesantes. Algunos, como Borja Cadenato, han propuesto duplicar la figura inicial pegando los dos triángulos por el lado donde no se apoyaba cuadrado, demostrando después que al unir consecutivamente los centros de los cuatro cuadrados obtenidos se obtiene a su vez otro cuadrado (resultado conocido como teorema de Thebault, como apuntaba Fernando Blasco en su solución). Otros, como Alejandro García Lampérez, han resuelto el desafío aplicando convenientemente el teorema del seno y el teorema del coseno. Y otros, muchos, han enviado demostraciones sintéticas distintas a la propuesta en el vídeo, entre los que podemos nombrar a Ignacio Larrosa y a Iago Vaamonde Paniagua (esta semana, en prosa).
Para finalizar, es de justicia valorar el trabajo de todas las personas que han enviado más de una solución, entre las que destacan Jesús Campos, que ha enviado cuatro soluciones distintas, y Sebastià Roig, que ha enviado cinco.
El jueves presentaremos el 40º y último desafío.
